MECÂNICA GERAL
Determine a massa da caixa sabendo que FAB = 1765,8 N; FAC = 882,9 N; FAD = 1765,8 N, numa condição de equilíbrio.
200 Kg
180 Kg
70 Kg
150 Kg
230 Kg
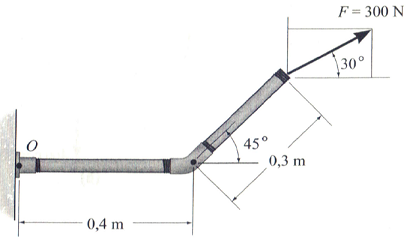
O momento de inércia da área de seção transversal da viga em relação ao eixo Y é APROXIMADAMENTE:
2,624 . 10 8 mm 4
7,924 . 10 8 mm 4
5,624 . 10 8 mm 4
2,937 . 10 8 mm 4
8,448 . 10 8 mm 4
Considerando a treliça dada a seguir,
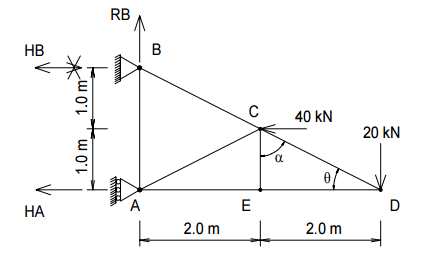
Determinando HA e HB , podemos admitir que
HA = 3HB .
HA = -3HB .
HA = HB .
3HB = 2HA .
HB = 2HA .
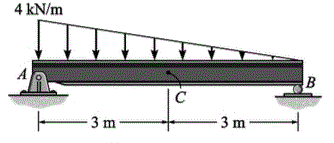
Qual o esforço cortante e momento em C.
VC = 5 kN
MC = -8 kN.m
VC = - 2 kN
MC = 7 kN.m
VC = - 1 kN
MC = 9 kN.m
VC = 5 kN
MC = 4 kN.m
VC = - 3 kN
MC = 10 kN.m
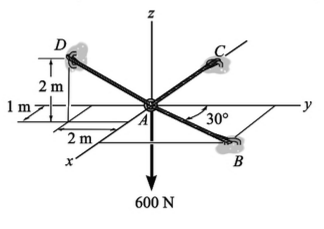
Determine a tração desenvolvida no cabo AB.
521 N
547 N
693 N
743 N
345 N
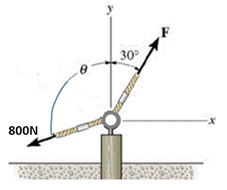
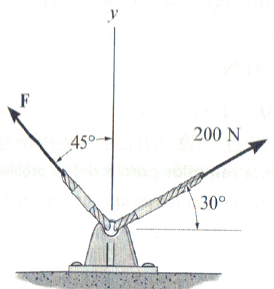
Determine a intensidade da força componente F na figura abaixo e a intensidade da força resultante se Fr estiver direcionada ao longo do eixo y positivo.
F = 129 N; Fr = 309 N
F = 245 N; Fr = 273 N
F = 157 N; Fr = 298 N
F = 225 N; Fr = 123 N
F = 271 N; Fr = 271 N
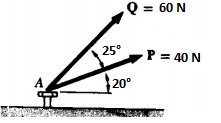
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:
97,7 N e 35 °
97,7 N e 30°
89,9 N e 35°
68,5 N e 30°
89,9 N e 22°
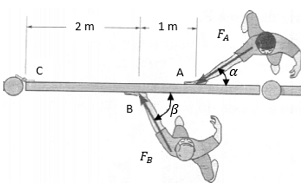
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 120 N, determine o valor aproximado da intensidade da força FA, que o garoto em A precisa exercer para que o portão não gire. Considere Alpha igual a 30° e Beta igual a 45°, despreze a espessura do portão.
200 Kg
180 Kg
70 Kg
150 Kg
230 Kg
O momento de inércia da área de seção transversal da viga em relação ao eixo Y é APROXIMADAMENTE:
2,624 . 10 8 mm 4
7,924 . 10 8 mm 4
5,624 . 10 8 mm 4
2,937 . 10 8 mm 4
8,448 . 10 8 mm 4
Considerando a treliça dada a seguir,

Determinando HA e HB , podemos admitir que
HA = 3HB .
HA = -3HB .
HA = HB .
3HB = 2HA .
HB = 2HA .
Qual o esforço cortante e momento em C.

VC = 5 kN
MC = -8 kN.m
VC = - 2 kN
MC = 7 kN.m
VC = - 1 kN
MC = 9 kN.m
VC = 5 kN
MC = 4 kN.m
VC = - 3 kN
MC = 10 kN.m
Determine a tração desenvolvida no cabo AB.

521 N
547 N
693 N
743 N
345 N
Determine a intensidade da força componente F na figura abaixo e a intensidade da força resultante se Fr estiver direcionada ao longo do eixo y positivo.

F = 129 N; Fr = 309 N
F = 245 N; Fr = 273 N
F = 157 N; Fr = 298 N
F = 225 N; Fr = 123 N
F = 271 N; Fr = 271 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

97,7 N e 35 °
97,7 N e 30°
89,9 N e 35°
68,5 N e 30°
89,9 N e 22°
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 120 N, determine o valor aproximado da intensidade da força FA, que o garoto em A precisa exercer para que o portão não gire. Considere Alpha igual a 30° e Beta igual a 45°, despreze a espessura do portão.

2,624 . 10 8 mm 4
7,924 . 10 8 mm 4
5,624 . 10 8 mm 4
2,937 . 10 8 mm 4
8,448 . 10 8 mm 4
Considerando a treliça dada a seguir,

Determinando HA e HB , podemos admitir que
HA = 3HB .
HA = -3HB .
HA = HB .
3HB = 2HA .
HB = 2HA .
Qual o esforço cortante e momento em C.

VC = 5 kN
MC = -8 kN.m
VC = - 2 kN
MC = 7 kN.m
VC = - 1 kN
MC = 9 kN.m
VC = 5 kN
MC = 4 kN.m
VC = - 3 kN
MC = 10 kN.m
Determine a tração desenvolvida no cabo AB.

521 N
547 N
693 N
743 N
345 N
Determine a intensidade da força componente F na figura abaixo e a intensidade da força resultante se Fr estiver direcionada ao longo do eixo y positivo.

F = 129 N; Fr = 309 N
F = 245 N; Fr = 273 N
F = 157 N; Fr = 298 N
F = 225 N; Fr = 123 N
F = 271 N; Fr = 271 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

97,7 N e 35 °
97,7 N e 30°
89,9 N e 35°
68,5 N e 30°
89,9 N e 22°
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 120 N, determine o valor aproximado da intensidade da força FA, que o garoto em A precisa exercer para que o portão não gire. Considere Alpha igual a 30° e Beta igual a 45°, despreze a espessura do portão.


HA = 3HB .
HA = -3HB .
HA = HB .
3HB = 2HA .
HB = 2HA .
Qual o esforço cortante e momento em C.

VC = 5 kN
MC = -8 kN.m
VC = - 2 kN
MC = 7 kN.m
VC = - 1 kN
MC = 9 kN.m
VC = 5 kN
MC = 4 kN.m
VC = - 3 kN
MC = 10 kN.m
Determine a tração desenvolvida no cabo AB.

521 N
547 N
693 N
743 N
345 N
Determine a intensidade da força componente F na figura abaixo e a intensidade da força resultante se Fr estiver direcionada ao longo do eixo y positivo.

F = 129 N; Fr = 309 N
F = 245 N; Fr = 273 N
F = 157 N; Fr = 298 N
F = 225 N; Fr = 123 N
F = 271 N; Fr = 271 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

97,7 N e 35 °
97,7 N e 30°
89,9 N e 35°
68,5 N e 30°
89,9 N e 22°
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 120 N, determine o valor aproximado da intensidade da força FA, que o garoto em A precisa exercer para que o portão não gire. Considere Alpha igual a 30° e Beta igual a 45°, despreze a espessura do portão.


VC = 5 kN
MC = -8 kN.m
VC = - 2 kN
MC = 7 kN.m
VC = - 1 kN
MC = 9 kN.m
VC = 5 kN
MC = 4 kN.m
VC = - 3 kN
MC = 10 kN.m
Determine a tração desenvolvida no cabo AB.

521 N
547 N
693 N
743 N
345 N
Determine a intensidade da força componente F na figura abaixo e a intensidade da força resultante se Fr estiver direcionada ao longo do eixo y positivo.

F = 129 N; Fr = 309 N
F = 245 N; Fr = 273 N
F = 157 N; Fr = 298 N
F = 225 N; Fr = 123 N
F = 271 N; Fr = 271 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

97,7 N e 35 °
97,7 N e 30°
89,9 N e 35°
68,5 N e 30°
89,9 N e 22°
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 120 N, determine o valor aproximado da intensidade da força FA, que o garoto em A precisa exercer para que o portão não gire. Considere Alpha igual a 30° e Beta igual a 45°, despreze a espessura do portão.


521 N
547 N
693 N
743 N
345 N
Determine a intensidade da força componente F na figura abaixo e a intensidade da força resultante se Fr estiver direcionada ao longo do eixo y positivo.

F = 129 N; Fr = 309 N
F = 245 N; Fr = 273 N
F = 157 N; Fr = 298 N
F = 225 N; Fr = 123 N
F = 271 N; Fr = 271 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

97,7 N e 35 °
97,7 N e 30°
89,9 N e 35°
68,5 N e 30°
89,9 N e 22°
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 120 N, determine o valor aproximado da intensidade da força FA, que o garoto em A precisa exercer para que o portão não gire. Considere Alpha igual a 30° e Beta igual a 45°, despreze a espessura do portão.

F = 129 N; Fr = 309 N
F = 245 N; Fr = 273 N
F = 157 N; Fr = 298 N
F = 225 N; Fr = 123 N
F = 271 N; Fr = 271 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

97,7 N e 35 °
97,7 N e 30°
89,9 N e 35°
68,5 N e 30°
89,9 N e 22°
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 120 N, determine o valor aproximado da intensidade da força FA, que o garoto em A precisa exercer para que o portão não gire. Considere Alpha igual a 30° e Beta igual a 45°, despreze a espessura do portão.


97,7 N e 35 °
97,7 N e 30°
89,9 N e 35°
68,5 N e 30°
89,9 N e 22°
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 120 N, determine o valor aproximado da intensidade da força FA, que o garoto em A precisa exercer para que o portão não gire. Considere Alpha igual a 30° e Beta igual a 45°, despreze a espessura do portão.